m_\pi-\div-m_k" class="header-anchor" href="#sterile-neutrinos-in-the-mass-range-$m_\pi-\div-m_k$"> Sterile neutrinos in the mass range $m_\pi \div m_K$

Interactions of sterile neutrinos mostly mimic the weak interactions of active neutrinos. However, non-zero mass of $N$ allows many channels previously forbidden by kinematics (e.g., $\nu \to \nu \nu \nu$ is forbidden, but $N \to \nu \nu \nu$ isn't).

In general, listing all leading order interactions of some particle requires building perturbation series for the corresponding Hamiltonian. This is a rather complicated task in case of the Standard Model, so it is convenient to use effective field theory ideas.

To account efficiently for all new interactions of sterile neutrinos with $m_N \ge m_\pi$, we need to list all possible effective interaction terms in the Lagrangian and take into consideration the thermodynamical state of the Universe at the moment of interest.

Primordial plasma

We consider the Early Universe at temperatures around few $MeV$. Plasma mostly consists of photons, active neutrinos, electrons and positrons - and tiny additions of long-living heavier particles like muons, protons and neutrons.

Thermodynamical state of the system is characterized by equilibrium in the electromagnetic sector (maintained by high-rate EM-interactions), while weakly-only interacting particles begin to decouple. This means that all weak processes rate are small comparing to the Hubble rate and it is possible to consider only few lowest orders in the weak expansion.

Additionally, we are interested only in the influence of interactions on non-equilibrium species as fast EM interactions dominate. Here is the tentative hierarchy of interaction rates:

$$\begin{equation} \Gamma_{EM} \gg H \ge \Gamma_{Weak} > \Gamma_{Sterile} \end{equation}$$

Processes of interest

For our discussion it is sufficient to consider only processes where only a single sterile neutrino is present. This narrows our list to processes of 2 kinds:

• $N \to 1 + 2 + \dotsc$
• $N + 2 \to 3 + 4 + \dotsc$

Kinematics

In case of sterile neutrino decay, allowed processes are limited solely the the masses of the final states:

$$\begin{align} p_N^\mu &= p_1^\mu + p_2^\mu + \dotsc \end{align}$$

Meaning that the mass of the sterile neutrino has to satisfy

$$\begin{equation} m_N \ge \sum_i m_i \end{equation}$$

Thus let's list all particles with masses below the Kaon mass:

The only states of interest are three pi-mesons composed of weakly interacting quark pairs. As they are relatively short-lived, abundant generation of them is improbable. Then, beside the previously considered processes, we need to anticipate the appearance of pions in the final states.

This leads to the following processes:

• Pionic decays: $$\begin{align} N &\to \nu_\alpha + \pi^0 \\\\ N &\to l^- + \pi^+ \end{align}$$
• Leptonic scatterings: $$\begin{align} N + \mu^+ \to K^+ \end{align}$$

Apparently, kaon reactions can appear already with $m_N > 388 MeV$, but we will see that interactions with kaons are suppressed by $|V_{us}|$ and the rareness of muons. Production of pions from leptonic scattering ($N + l^+ \to \pi^+$) is forbidden by kinematics.

The backreaction of the pions on the plasma is dominated by few decay modes:

$$\begin{align} \pi^0 &\to \gamma + \gamma \\\\ \pi^+ &\to \mu^+ + \nu_\mu \\\\ \pi^+ &\to e^+ + \nu_e \end{align}$$

Pion interactions

According to the quark model, mesons are bound states formed by quark pairs and gluons. In practice this means that quark quantum states inside mesons are deformed and one cannot directly apply the Feynman calculus. However, in case of electroweak interactions, only the quarks carry the corresponding quantum numbers and the influence of gluons can be omitted.

Phenomenological model

According to experimental evidence, pi-mesons constitute a pseudoscalar triplet. Simplest possible interactions for a pion with fermionic current then have to be of the form

$$\begin{align} g J_\mu^{\pm(0)} F^\mu + g' \overline{f} \gamma^5 \pi f \end{align}$$

The latter interaction is not realized in nature (proven by experiments and can be explained from theoretical point of view by Goldstone boson-like origin of the pions).

$F^\mu$ is referred to as the "pion form-factor". It's precise form can be reconstructed by recalling that for a spin-0 particle the only associated 4-vector is it's momentum. Moreover, multiplier of this vector has to be a Lorentz scalar, thus depending only on the $p^2 = m_\pi^2$. However, this multiplier can differ for neutral and charged pions.

$$\begin{equation} F^\mu = f_\pm p^\mu \end{equation}$$

Gauge bosons interactions

According to the phenomenological model, pi-mesons is gradiently coupled to SM currents, thus we assume that this interaction has a form analogous to the regular current interactions. In particular, we can apply Feynman rules for quarks and fix the renormalization due to gluons using the observed lifetime of the meson.

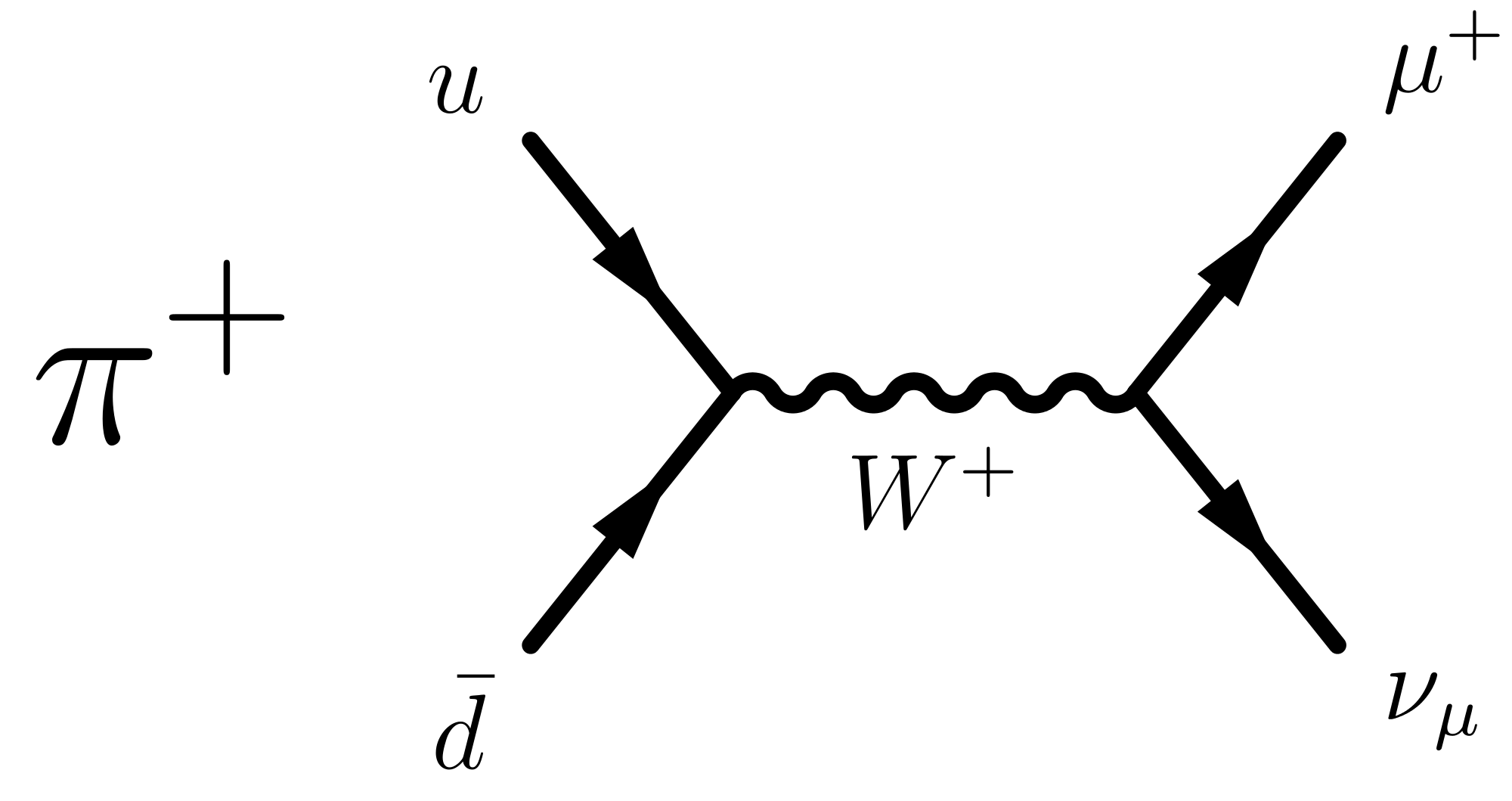
Feynman rules

$$\begin{align} \Delta \mathcal{L}\_{CC} = \frac{g}{2 \sqrt{2}} \begin{bmatrix} \overline{u} & \overline{c} & \overline{t} \end{bmatrix} \gamma^\lambda (1-\gamma^5) V_{CKM} \begin{bmatrix} d \\\\ s \\\\ b \end{bmatrix} W_\lambda^+ + h.c. \end{align}$$

$$\begin{align} \Delta \mathcal{L}\_{NC} = \frac{g}{\cos \theta_W} \left( \epsilon_L^{(f)} \overline{f}_L \gamma^\lambda f_L + \epsilon_R^{(f)} \overline{f}_R \gamma^\lambda f_R \right) Z\_\lambda \end{align}$$

where

$$\begin{align} \epsilon_L^{(f)} &= -\frac12 - Q_f \sin^2 \theta_W && \text{for} &f = e,\mu,\tau,d,s,b \\\\ \epsilon_L^{(f)} &= +\frac12 - Q_f \sin^2 \theta_W && \text{for} &f = \nu_e,\nu_\mu,\nu_\tau,u,c,t \\\\ \epsilon_R^{(f)} &= - Q_f \sin^2 \theta_W \end{align}$$

or

$$\begin{align} \Delta \mathcal{L}\_{NC} = \frac{g}{\cos \theta_W} \overline{f} \gamma^\lambda (v_f - a_f \gamma^5) f \; Z\_\lambda \end{align}$$

$$\begin{align} v_f = \pm_f \frac14 - Q_f \sin^2 \theta_W && a_f = \pm_f \frac14 \end{align}$$

$$\begin{align} \begin{cases} \pm_f = -1 && \text{for} &f = e,\mu,\tau,d,s,b \\\\ \pm_f = +1 && \text{for} &f = \nu_e,\nu_\mu,\nu_\tau,u,c,t \end{cases} \end{align}$$

Direct interaction of the pion states with bosons is considered to be

$$\begin{align} \Delta \mathcal{L}\_{\pi W} &= \frac{g}{2\sqrt{2}} f_\pm |V_{ud}| (\partial_\mu \pi) {W^\dagger}^\mu + h.c. \\\\ \Delta \mathcal{L}\_{\pi Z} &= \frac{g}{2 \cos \theta_W} f_0 (\partial_\mu \pi^0) Z^\mu \end{align}$$

Turns out that $f_\pm = \sqrt{2} f_0 = f_{\pi} \approx 130 MeV$

Relation between $f_\pm$ and $f_0$ can be related to the fact that precise quark composition of the $\pi^0$ is $\frac{1}{\sqrt{2}}(u \overline{u} + d \overline{d})$

Matrix elements

Pions production

$$\begin{align} N &\to \pi^0 + \nu_\alpha \\\\ \overline{\nu}_\alpha + N &\to \pi^0 \\\\ N &\to \pi^+ + l^- \\\\ l^+ + N &\to \pi^+ \end{align}$$

We will concentrate on computation of the first diagram and will get to the others by a series of substitutions. In the following, $\nu$ spinor represents the lepton and $N$ is a sterile neutrino.

$$\begin{align} \require{cancel} \imath \mathcal{M} &= \left( \overline{\nu}(k) \gamma^\mu \frac{-\imath g'}{2} \frac{1+\gamma^5}{2} \frac{\imath}{\cancel{p}} M_D N(p) \right) \frac{-\imath g_{\mu \nu}}{M_Z^2} \left( \frac{g'}{2\sqrt{2}} f_\pi \pi^\nu \right) = \\\ &= -\imath \frac{g'^2 M_D f_\pi}{4 \sqrt{2} M_Z^2} \overline{\nu}(k) \cancel{\pi} \frac{1+\gamma^5}{2} \frac{\cancel{p}}{p^2} N(p) = -\imath \frac{g'^2 M_D f_\pi}{4 \sqrt{2} m_N^2 M_Z^2} \overline{\nu}(k) \cancel{\pi} \frac{1+\gamma^5}{2} \cancel{p} N(p) \end{align}$$

$$\begin{align} \require{cancel} |\mathcal{M}|^2 &= \frac{g'^4 M_D^2 f_\pi^2}{32 m_N^4 M_Z^4} \left( \overline{\nu}(k) \cancel{\pi} \frac{1+\gamma^5}{2} \cancel{p} N(p) \right) \left( \overline{N}(p) \cancel{p} \frac{1-\gamma^5}{2} \cancel{\pi} \nu(k) \right) = \left(\frac{g'}{M_Z}\right)^4 \frac{M_D^2 f_\pi^2}{32 m_N^4} Tr\left[ \nu \overline{\nu} \cancel{\pi} (\frac{1+\gamma^5}{2}) \cancel{p} N \overline{N} \cancel{p} (\frac{1-\gamma^5}{2}) \cancel{\pi} \right] \end{align}$$

Averaging by sterile neutrino polarizations and summing by neutrino's:

$$\begin{align} \require{cancel} |\mathcal{\overline{M}}|^2 &= \left(\frac{g'}{M_Z}\right)^4 \frac{M_D^2 f_\pi^2}{32 m_N^4} Tr\left[(\cancel{k} \pm m_l) \cancel{\pi} (\frac{1+\gamma^5}{2}) \cancel{p} (\cancel{p} \pm m_N) \cancel{p} (\frac{1-\gamma^5}{2}) \cancel{\pi} \right] \end{align}$$

The $\pm m_N$ sign comes from the spin sum for Majorana fermion that is not defined. Fortunately, chirality projectors automatically remove the constant term of that spin sum.

The sign in the lepton spin sum depends on the side, where this particle occurs in the reaction. For the outgoing lepton it will be $+$ and $-$ for incoming antilepton. However, lepton mass occurs only in a term with an odd number of gamma matrices in a trace - hence, it vanishes.

Reaction kinematics

$$\begin{align} &p^\mu = k^\mu + \pi^\mu \\\ &\begin{cases} p^2 &= m_N^2 = (p \cdot k) + (p \cdot \pi) \\\ (p \cdot k) &= k^2 + (k \cdot \pi) = m_l^2 + (k \cdot \pi) \\\ (p \cdot \pi) &= (k \cdot \pi) + \pi^2 = (k \cdot \pi) + m_\pi^2 \end{cases} \\\ &\begin{cases} (p \cdot k) &= \frac12 (m_N^2 + m_l^2 - m_\pi^2) \\\ (p \cdot \pi) &= \frac12 (m_N^2 - m_l^2 + m_\pi^2) \end{cases} \end{align}$$

Trace computation

As the trace expression is the same between both diagrams, we will compute it in assumption $m_l \neq 0$

$$\begin{align} \require{cancel} Tr &= m_N^2 Tr\left[ \cancel{k} \cancel{\pi} \frac{1+\gamma^5}{2} \cancel{p} \cancel{\pi} \right] = m_N^2 Tr\left[ (\cancel{p}-\cancel{\pi}) \cancel{\pi} \frac{1+\gamma^5}{2} \cancel{p} \cancel{\pi} \right] \\\\ &= m_N^2 Tr\left[ \cancel{p} \cancel{\pi} \frac{1+\gamma^5}{2} \cancel{p} \cancel{\pi} \right] - m_N^2 m_\pi^2 Tr\left[ \frac{1+\gamma^5}{2} \cancel{p} \cancel{\pi} \right] \\\\ &= - 2 m_N^4 m_\pi^2 + 4 m_N^2 (p \cdot \pi)^2 - 2 m_N^2 m_\pi^2 (p \cdot \pi) \\\\ &= - 2 m_N^4 m_\pi^2 + m_N^2 (m_N^2 - m_l^2 + m_\pi^2)^2 - m_N^2 m_\pi^2 (m_N^2 - m_l^2 + m_\pi^2) \\\\ &= m_N^4 (m_N^2 - m_\pi^2) - m_l^2 m_N^2 (2 m_N^2 + m_\pi^2 - m_l^2) \end{align}$$

Neutral current and neutrino scattering

Putting that back to the squared amplitude with $m_l = 0$

$$\begin{align} \require{cancel} |\mathcal{\overline{M}}|^2 &= \left(\frac{g'}{M_Z}\right)^4 \frac{M_D^2 f_\pi^2}{32} (m_N^2 - m_\pi^2) = G_F^2 M_D^2 f_\pi^2 (m_N^2 - m_\pi^2) = G_F^2 \theta^2 f_\pi^2 m_N^2 (m_N^2 - m_\pi^2) \end{align}$$

Charged current and lepton scattering

For the diagrams with charged leptons we need to include the mass of the lepton and modify the coupling constants ($g' \to g$, $M_Z \to M_W$ and multiply the whole amplitude by $|V_{ud}|$)

$$\begin{align} \require{cancel} |\mathcal{\overline{M}}|^2 &= G_F^2 \theta^2 |V_{ud}|^2 f_\pi^2 \left[ (m_N^2 -m_l^2)^2 - m_\pi^2 (m_N^2 + m_l^2) \right] \end{align}$$